물질파 (드브로이파) - 수험생 물리

[광전효과]와 함께 [컴프턴효과]는 빛의 입자적 성질을 보여주는 대표실험입니다. 빛의 순수히 파동의 성질만 가지고 있는게 아니라 입자적 성질도 가지고 있다면, 혹시 입자적 성질만 보았던 물체의 움직임에도 파동의 성질이 있지 않을까요?

물질의 파동적 성질

드브로이(de Broglie)가 왜, 어떻게 그런 생각을 하게 되었는지 모르지만, 빛이 이중적 성질이 있는 것 같이 물질도 이중적 성질을 가지고 있을 것라고 생각했습니다. 그 파동을 물질파(物質波, matter wave) 또는 드브로이파(de Broglie wave)라고 합니다.

광자의 에너지 E, 운동량 p 를 구하라고 하면

E = h/T = h f ( f는 진동수로 1/T )

p = h/\( \lambda \) = h k ( k 는 파수로 1/\( \lambda \))

라고 하는 것과 완전히 대칭적으로

물질파의 주기 T, 파장 \( \lambda \) 을 구하라고 하면

T = h/E ( E = 1/2mv^2 과 같은 운동에너지일 수 있습니다. 물론 아주 빠르다면 상대성 이론도 생각해야합니다.)

\( \lambda \) = h/p (p=mv 와 같은 운동량이겠지만, 아주 빠르다면 상대성 이론도 생각해야합니다.)

라고 생각하는 것입니다.

물질파?

우리가 평소에 알고 있던 파동이 물질의 파동입니다. 예를 들어 파도는 물의 파동입니다. 소리는 공기의 파동입니다. 물질이 원래 파동의 성질이 있는것 아닌가요? 물질파(드브로이파)와는 뭐가 다른가요?

물질파(드브로이파)에서 말하는 파동은 기존의 파동에서 이야기하는 것과는 다릅니다. 입자로 해석하던 물체의 움직임을 파동처럼 설명하자는 것입니다. 물체의 움직으로 입자로 해석하는 것은 물체가 움직이면 어딘가 도착하고 충돌하여 튕겨져 나오는 현상 등 물리를 처음 배울 때 움직임을 해석하던 그 방법들을 말합니다. 그렇게 움직이는 것을 파동처럼 생각할 수 있다는 것입니다. 파동시간에 배운 파동은 물체는 제자리에서 흔들거리고 에너지를 전파하는 것이지 직접 움직이는 게 아니라고 했습니다. 그러니, 물질파는 기존에 배운 파동과는 다른 내용입니다. 이제는 제자리에서 진동하는 것이 말고 물체의 이동하는 것 마저도 마치 파동같다니 도대체 뭔말인지 알 수가 없습니다.

그러게요..
아무리 말로 설명하려고 해도 잘 못하는 것은 제 실력이 좋지 않기 때문입니다. 그러니, 실험을 보면서 나타난 현상을 알려드리겠습니다.

입자로는 설명하기 어렵고 파동으로만 설명가능 한 대표적 현상이 회절, 간섭입니다. 물질파가 존재한다면 그런 회절,간섭현상이 보여야할 것입니다. 물리학자들도 물질파를 믿으려면 그런 증거를 보아야하지 않겠습니까? 그런 실험들을 통해 드브로이의 생각이 맞는지 검증을 하는 것입니다.

[컴프턴효과] 에서 X선의 파동의 성질을 설명할 때 고체에 X선을 쪼이면 X선의 회절,간섭에 의한 무늬를 볼 수 있다고 했습니다. 만약 전자의 물질파(드브로이파)의 파장을 X선의 파장과 같게 만들어서 고체에 전자를 쏘면 X선의 회절 무늬와 똑같은 무늬를 얻을 수 있어야 할 것입니다. 교과서나 인터넷에에 그런 무늬 그림이 나옵니다만 공개된 데이터는 구하지 못해서 못 보여드리네요.

뿐만 아니라 회절 실험의 대표실험인 이중슬릿의 무늬와 같은 것을 전자를 이용해서도 할 수 있을 것입니다. 전자는 입자입니다. 그러니까, 총처럼 전자를 쏘아주면 이중 슬릿을 지나 반대편 스크린에 떨어집니다. 그렇게 전자가 떨어진 곳이 밝게 빛나는 사진을 찍은 것입니다.

(이 그림의 출처 및 저작권 정보는 다음과 같습니다. https://commons.wikimedia.org/wiki/File:Double-slit.svg )

그 이중슬릿 실험 결과를 구했습니다.

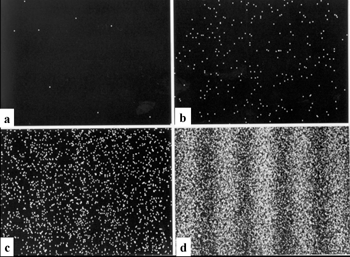
(이 사진의 출처 및 저작권 정보는 다음과 같습니다. https://commons.m.wikimedia.org/wiki/File:Doubleslitexperiment_results_Tanamura_1.gif)

그림의 (a)는 전자를 8개 쏘았습니다. 8개의 점이 나타납니다. 각 점마다 전자가 입자인 것이 잘 드러납니다. 여기 무슨 파동의 성질이 보입니까? 전혀 보이지 않습니다. 그냥 8개의 점이 있습니다.

그러나, 그 갯수를 점점 늘려갑니다. (b)는 270 개 입니다. (c)는 2000개 입니다. (d)는 6000개입니다. (d) 를 보니 두 개의 가는 선이 나타나는 게 아니라 마치 이중슬릿 회절 무늬와 같이 나타나는 것입니다.

> 여기는 자료가 없지만, 전자의 속력을 잘 조정하면 물질파의 파장이 바뀔 것입니다. 그러면 이 무늬의 간격도 바뀔 것입니다. 이 실험에서는 전자의 속력은 모두 똑같게 잘 만들어 둔 실험입니다.

이런 사진들이 물질파가 존재한다는 증거입니다. 이런 것과 비슷한 실험은 21세기가 들어서도, 전자가 아닌 것에서도 나타난다는 실험들은 계속 보여지고 있습니다. [Wave–particle duality](https://en.wikipedia.org/wiki/Wave%E2%80%93particle_duality)에서 Wave nature of large objects 란 부분에 보면 나열 되어 있습니다.

물질파를 파동함수로 표현하기

물질파의 파장은 \( \lambda \) = h/p = h /(mv) , 진동수 f = E/h = (1/2mv^2)/h 가 된다면 파동의 속력은 f \( \lambda \) = v/2 가 되잖아. 이거 뭐야?

상대성 이론을 따져야 하나?

\( \lambda = h/p = h /(mv) \)

\( f = E/h = (mc^2)/h \)

파동의 속력은 \( f \lambda = c^2/v \)

또 이건 뭐야? 빛보다 무지하게 빠른 속력인데..?

속력 v 가 제대로 나오지 않습니다. 이렇게 막상 파장과 진동수를 구하려고 해 보아도 이상한 결과에 이르는 것은 물질파를 단순한 sin 함수라고 가정하고 문제를 접근하고 있기때문입니다. 파동에서 설명드렸다시피 파동을 sin 함수로 설명하는 것은 파동을 쉽게 이해하기 위한 것이지, 파동이 반드시 단순한 sin 함수는 아닙니다. 일반적으로 파동은 많은 sin 함수들의 합으로 복잡한 모양입니다.

이렇게 복잡한 물질파의 파동함수를 찾아내려면 어떻게 알 수 있을까요? 그런 파동함수를 찾아내는 방법 중 하나가 슈뢰딩거 방정식(Schrödinger equation)을 푸는 것입니다.

> 요즘 좀 어려운 시험에서는 이 파동함수까지 물어 보는 문제가 출제됩니다. 제가 보기에는 좀 과도한게 아닌가란 생각이 듭니다. 전공자에게는 아주 쉬운 경우일지 모르지만 양자역학을 처음 배우는 일반물리/대학물리에서는 그냥 외어 풀어야하는 황당한 문제일 뿐입니다.